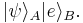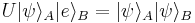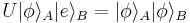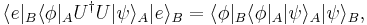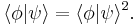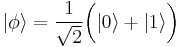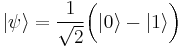No-cloning theorem
| Quantum mechanics |
|---|
 |
| Introduction Glossary · History |
|
Background
|
|
Fundamental concepts
|
|
Formulations
|
|
Equations
|
|
Advanced topics
|
|
Scientists
Bell · Bohm · Bohr · Born · Bose
de Broglie · Dirac · Ehrenfest Everett · Feynman · Heisenberg Jordan · Kramers · von Neumann Pauli · Planck · Schrödinger Sommerfeld · Wien · Wigner |
The no-cloning theorem is a result of quantum mechanics that forbids the creation of identical copies of an arbitrary unknown quantum state. It was stated by Wootters, Zurek, and Dieks in 1982, and has profound implications in quantum computing and related fields.
The state of one system can be entangled with the state of another system. For instance, one can use the Controlled NOT gate and the Walsh-Hadamard gate to entangle two qubits. This is not cloning. No well-defined state can be attributed to a subsystem of an entangled state. Cloning is a process whose end result is a separable state with identical factors.
Contents |
Proof
Suppose the state of a quantum system A, which we wish to copy, is 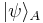 (see bra-ket notation). In order to make a copy, we take a system B with the same state space and initial state
(see bra-ket notation). In order to make a copy, we take a system B with the same state space and initial state 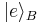 . The initial, or blank, state must be independent of
. The initial, or blank, state must be independent of 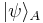 , of which we have no prior knowledge. The composite system is then described by the tensor product, and its state is
, of which we have no prior knowledge. The composite system is then described by the tensor product, and its state is
There are only two ways to manipulate the composite system. We could perform an observation, which irreversibly collapses the system into some eigenstate of the observable, corrupting the information contained in the qubit. This is obviously not what we want. Alternatively, we could control the Hamiltonian of the system, and thus the time evolution operator U (for time independent Hamiltonian, 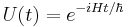 , and
, and 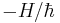 is called the generator of translations in time) up to some fixed time interval, which yields a unitary operator. Then U acts as a copier provided that
is called the generator of translations in time) up to some fixed time interval, which yields a unitary operator. Then U acts as a copier provided that
and
for all 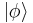 and
and 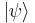 . By definition of unitary operator, U preserves the inner product:
. By definition of unitary operator, U preserves the inner product:
i.e.
This implies that either 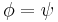 or
or  is orthogonal to
is orthogonal to  which is not true in general. While orthogonal states in a specifically chosen basis
which is not true in general. While orthogonal states in a specifically chosen basis 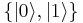 , for example:
, for example:
and
fit the requirement that 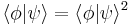 , this result does not hold for more general quantum states. Apparently U cannot clone a general quantum state. This proves the no-cloning theorem.
, this result does not hold for more general quantum states. Apparently U cannot clone a general quantum state. This proves the no-cloning theorem.
Generalizations
Mixed states and nonunitary operations
In the statement of the theorem, two assumptions were made: the state to be copied is a pure state and the proposed copier acts via unitary time evolution. These assumptions cause no loss of generality. If the state to be copied is a mixed state, it can be purified. Similarly, an arbitrary quantum operation can be implemented via introducing an ancilla and performing a suitable unitary evolution. Thus the no-cloning theorem holds in full generality.
Arbitrary sets of states
Non-clonability can be seen as a property of arbitrary sets of quantum states. If we know that a system's state is one of the states in some set S, but we do not know which one, can we prepare another system in the same state? If the elements of S are pairwise orthogonal, the answer is always yes: for any such set there exists a measurement which will ascertain the exact state of the system without disturbing it, and once we know the state we can prepare another system in the same state. If S contains two elements that are not pairwise orthogonal (in particular, the set of all quantum states includes such pairs) then an argument like that given above shows that the answer is no.
The cardinality of an unclonable set of states may be as small as two, so even if we can narrow down the state of a quantum system to just two possibilities, we still cannot clone it in general (unless the states happen to be orthogonal).
Another way of stating the no-cloning theorem is that amplification of a quantum signal can only happen with respect to some orthogonal basis. This is related to the emergence of classical probability rules in quantum decoherence.
No-cloning in a classical context
There is a classical analogue to the quantum no-cloning theorem, which we might state as follows: given only the result of one flip of a (possibly biased) coin, we cannot simulate a second, independent toss of the same coin. The proof of this statement uses the linearity of classical probability, and has exactly the same structure as the proof of the quantum no-cloning theorem. Thus if we wish to claim that no-cloning is a uniquely quantum result, some care is necessary in stating the theorem. One way of restricting the result to quantum mechanics is to restrict the states to pure states, where a pure state is defined to be one that is not a convex combination of other states. The classical pure states are pairwise orthogonal, but quantum pure states are not.
Consequences
- The no-cloning theorem prevents us from using classical error correction techniques on quantum states. For example, we cannot create backup copies of a state in the middle of a quantum computation, and use them to correct subsequent errors. Error correction is vital for practical quantum computing, and for some time this was thought to be a fatal limitation. In 1995, Shor and Steane revived the prospects of quantum computing by independently devising the first quantum error correcting codes, which circumvent the no-cloning theorem.
- Similarly, cloning would violate the no teleportation theorem, which says classical teleportation (not to be confused with entanglement-assisted teleportation) is impossible. In other words, quantum states cannot be measured reliably.
- The no-cloning theorem does not prevent superluminal communication via quantum entanglement, as cloning is a sufficient condition for such communication, but not a necessary one. Nevertheless, consider the EPR thought experiment, and suppose quantum states could be cloned. Assume parts of a maximally entangled Bell state are distributed to Alice and Bob. Alice could send bits to Bob in the following way: If Alice wishes to transmit a "0", she measures the spin of her electron in the z direction, collapsing Bob's state to either
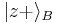 or
or 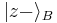 . To transmit "1", Alice does nothing to her qubit. Bob creates many copies of his electron's state, and measures the spin of each copy in the z direction. Bob will know that Alice has transmitted a "0" if all his measurements will produce the same result; otherwise, his measurements will have outcomes +1/2 and −1/2 with equal probability. This would allow Alice and Bob to communicate across space-like separations.
. To transmit "1", Alice does nothing to her qubit. Bob creates many copies of his electron's state, and measures the spin of each copy in the z direction. Bob will know that Alice has transmitted a "0" if all his measurements will produce the same result; otherwise, his measurements will have outcomes +1/2 and −1/2 with equal probability. This would allow Alice and Bob to communicate across space-like separations.
- The no cloning theorem prevents us from viewing the holographic principle for black holes as meaning we have two copies of information lying at the event horizon and the black hole interior simultaneously. This leads us to more radical interpretations like black hole complementarity.
Imperfect cloning
Even though it is impossible to make perfect copies of an unknown quantum state, it is possible to produce imperfect copies. This can be done by coupling a larger auxiliary system to the system that is to be cloned, and applying a unitary transformation to the combined system. If the unitary transformation is chosen correctly, several components of the combined system will evolve into approximate copies of the original system. Imperfect cloning can be used as an eavesdropping attack on quantum cryptography protocols, among other uses in quantum information science.
See also
- Fundamental Fysiks Group
- No-broadcast theorem
- Quantum entanglement
- Quantum cloning
- Quantum information
- Quantum no-deleting theorem
- Quantum teleportation
- Uncertainty principle
References
Other sources
- W.K. Wootters and W.H. Zurek, A Single Quantum Cannot be Cloned, Nature 299 (1982), pp. 802–803.
- D. Dieks, Communication by EPR devices, Physics Letters A, vol. 92(6) (1982), pp. 271–272.
- V. Buzek and M. Hillery, Quantum cloning, Physics World 14 (11) (2001), pp. 25–29.